徐光启、利玛窦与《几何原本》（五）

上篇从序文分析了《几何原本》是起源自中国名家、墨家，逐代累积而成的一部数学著作，它有非常广泛的应用场景。而一位网友在评论中说“柏拉图追求纯粹的数学，严禁数学用于机械制造”，而我读完《几何原本》后恰恰认为这是一部完完全全的应用之书。

徐光启的六卷版（下称徐版），对照白话文/英文（下称欧版）来看，会有巨大的收获。

題論之首。先標界說。次設公論題論所據。次乃具題。題有本解。有作法。有推論。先之所徵。必後之所恃。十三卷中。五百餘題。一脈貫通。——徐光启

首先是界说，先对所研究的名目进行定义。

第一界 点者无分。无长短广狭厚薄。

相信有初中文化水平的都能读懂这个定义的内容。

对比下欧版

01/点是没有部分的东西

A point is that which has no part.

嗯……无论是英文还是中文白话都不是人话。并且徐版对“点者无分”做了进一步解释，“无长短广狭厚薄”。这欧版怎么没了？

再看下一个：

第二界 线有长无广。试如一平靣，光照之，有光无光之间，不容一物，是线也。真平真圆相遇，其相遇处止有一点，行则止有一线。线有直有曲。

这里不仅定义了线没有宽度，并给出了两个具体的形象，且涵盖了直线和曲线。

圆与平面的切点是一个点，这个点运行的轨迹是线。这个具体形象体现了中国人在定义线这个概念时的思维路径，点运行的轨迹是线，即线是点的积分。

而欧版呢？只剩下：

02/线是没有宽的长。

A line is breadthless length.

徐版的内容比欧版要详尽的多，准确的多。怎么会有翻译版比原版内容更丰富、逻辑更顺畅呢？那么这个是翻译了一本书还是创作了一本书呢？

再看第四界

第四界 直线止有两端。两端之间，上下更无一点。两点之间至径者直线也，稍曲则绕而长矣。直线之中点能遮两界。凡量逺近皆用直线。

这就是我们初中学的“两点之间直线最短”。可是到了欧版，竟然变成了：

04/直线是其上均放置着点的线

A straight line is a line which lies evenly with the points on itself.

很显然这个直线定义就是错误的，曲线也是“其上均放置着点的线”啊。这和两点之间直线最短也没有任何关系啊，徐光启是如何通过错误的原著翻译出正确的结论的呢？

第五界　靣者止有长有广。体所见为靣。凡体之影极似于靣【无厚之极】。想一线横行所留之迹即成靣也。

面的定义也体现了积分的思想，即一线横行所留之迹。而欧版呢？

05 / 面是只有长和宽的东西。

A surface is that which has length and breadth only.

由含混翻译成精准，由简陋翻译成详细，由错误翻译成正确。才看了5个定义，仅从字面上就可以看出徐版描述的准确性、逻辑性、思想深度都是高于欧版的。高中英语水平也能看出这样的中文表述不可能来自这样简略的英文（拉丁文）翻译，《几何原本》不可能出自欧几里得版的翻译，是中国的原创著作。而这种含混、错误在欧版《几何原本》中比比皆是。

看到这里不知道各位读者是什么感受，我个人在仅看完三页半《几何原本》原文后是震惊的。如此明显的问题400年来我们的专业学者都不曾质疑过，我们就天真的相信这本书是从外国人那里翻译来的。我们的学术平台上有几百篇研究《几何原本》的学术论文，竟然没有一篇提及过这个问题。我们的文史学者们都在做什么呢？

界说之后是求作，欧版称之为公设。徐版和欧版差别在于第四求。

徐版的第四求讨论了度与数的关系。数可以无限大，但最小只能是1。度可大可小，可以无限大也可以无限小。这就解决了没有小数的问题，即只要度量单位足够小，就可以解决小于1的数学问题。

在阐述度如何能够无穷小时，引用了庄子所言“一尺之棰日取其半万世不竭”，这体现了分数的概念以及无穷小的概念，这就是微分啊。西方人说中国人没有发明微积分，实际上从庄子到徐光启无穷小的概念都是存在于中国人的数学思想中的。

第四求在欧版里不存在，而我认为这恰恰是《几何原本》最核心的内容，他在讨论度与数的关系，度是刻度、测量精度，数是数值、测量值。《几何原本》是探讨在一定测量精度下的几何数问题。而测量精度就是一个应用问题，需要考虑在实际工作中使用的尺规的精准度、度量单位，《几何原本》是在应用中产生并用来指导生产实践的书籍。

“凡言度者或线或面或体皆是”这里对度的定义不包含点，而点的定义是“点者无分”，正因为点是不可再分的，所以它不能“日取其半万世不竭”。可见徐版《几何原本》对于概念的定义是极其精准且一以贯之的。而这种思想在欧版中是不存在的。

点是没有部分的东西。。。。？

欧版的第四、第五公设是直接把后面一章公论十九则的第十、第十一公论提前了。

西方人吹嘘《几何原本》的第五公设（第11论），却绝口不提徐光启的第四求。第四求比第五公设高级一万倍。而且这是中文版《几何原本》独有的，欧洲人根本读不懂，所以就硬把后面的一页提前到这了。还因此以讹传讹造出一个第五公设的狗血剧情，却不知道之所以第五公设放在这里这么突兀，完全就是因为抄！错！了！！！

由于第四求欧洲人没看懂，又导致了公论中的第十四到十九论也看不懂，所以12-19论直接被删掉了。徐版第一卷的公论有十九条，欧版的公理只剩下五条。哪个是原著，哪个是翻译版，不言自明。

第十四论到第十九论讨论了“几何度”问题。何为几何度？与度有什么区别？几何度指的是在某一精度下测得的量，这沿袭了第四求所讨论的度与数的思想，涵盖了测度的概念，这是专门为指导应用实践而探讨的问题。欧洲人因为看不懂第四求，也就不能理解几何度，因此西方数学产生了很多悖论和混乱，比如测度为0的情况，而徐光启的《几何原本》是以测量实践为基础的，测度＞0是讨论问题的前提。

看完了定义、公设、公理，终于开始刷题了。我们以第十二题为例对比一下徐版和欧版的差别。

这个题目是直线外一点如何作垂线，徐版就像徐光启在序中所说的有本解、有推论，还列举了两种用法。先论证了线外一点丙做圆与直线相交的两点丁戊，丁戊之间的中点与丙的连线就是垂线。再介绍了以最简便的做圆的方式如何确定中点以及这条垂线。不但有逻辑推理，还有实践应用。这验证了他在序中所说的应用场景（农业、建造、机器、水利等等）。

而欧版呢？只证明了GE中点连线就是垂线。但是如何去确定一个线段的中点呢？没有。

题目是求作垂线，答案是与中点的连线就是垂线，那怎么找到中点就不提了，靠手量吗？一边五拃？

13卷欧版《几何原本》全部题目都只有证明，没有用法。

回忆一下我们的几何教科书，你会发现《几何原本》与我们的教科书题目的不同点：我们教科书题目是给定条件，要求证明或计算一个未知量。即已知H是GE中点，证明CH⊥GE。这是一道证明题。而《几何原本》的题目是求作过直线外一点的垂线，这是一道应用题。

在《几何原本》中有大量这样的应用题，比如求作垂线、求作正方形、求作圆外切形、求作圆内切三角形、五边形、六边形、十五边型等等。它是以实际应用为目的，要求学生自己发现条件并寻找解决方法。学习几何的目的是为了应用于实际工作，《几何原本》是一本应用之书。西方人宣称欧几里得追求纯粹的数学，却忘记了书里都是应用题。

我们今天所沿袭的西方教育体系恰恰存在理论脱离实际的问题，学生读了十几年的书，毕业后基本等同于一个废人，基本生活能力没有，解决问题的能力也没有。其根源就是我们对西方科学体系、对《几何原本》的误读，而几何（科学）的原本恰恰就是为解决实际问题而存在的。

扯远了，继续说《几何原本》。

前四卷在介绍点线面角形的定义与关系，第五、六卷开始介绍比例。也就是在讨论测度的换算、单位的换算、比例的换算。显然这是应用中必修的知识，制图建造不就是不同尺度不同维度的等比例缩放吗？

举例说明，第五卷第一界

第一界 分者，几何之几何也。小能度大。以小为大之分。

小能度大，就是以小精度去测量大长度。所谓的比例、分数概念就产生于测量应用之中。比例问题仍然是在研究度与数，即精度与长度的关系。

01 / 当较小量量尽较大量时，较小量是较大量的一个部分。

A magnitude is a part of a magnitude, the less of the greater, when it measures the greater.

看看欧版，他们也知道这个是来自测量。瞒不住啊。

接下来第三界定义了有理数和无理数：

凡比例有二种，有大合、有小合。以数可明者为大合，如二十尺之线比十尺之线是也。其非数可明者为小合。如直角方形之两邉与其对角线可以相比而非数可明者是也。

如上二种，又有二名：其大合线为有两度之线，如二十尺比八尺两线为大合，则二尺四尺皆可两度之者是也。如此之类凡数之比例皆大合也。何者？有数之属或无他数可两度者无有一数不可两度者。若七比九无他数可两度之，以一则可两度之也。其小合线为无两度之线。如直角方形之两邉与其对角线为小合，即分至万分以及无数终无小线可以尽分能度两率者是也。

对于无理数显然也是通过实践观察到了直角三角形的弦是无法取尽的小数，但在现实中是会出现的，因此定义了无理数（小合）。这里还是出于度量的考虑，同理也包括圆周率。

欧版这些定义都不存在。

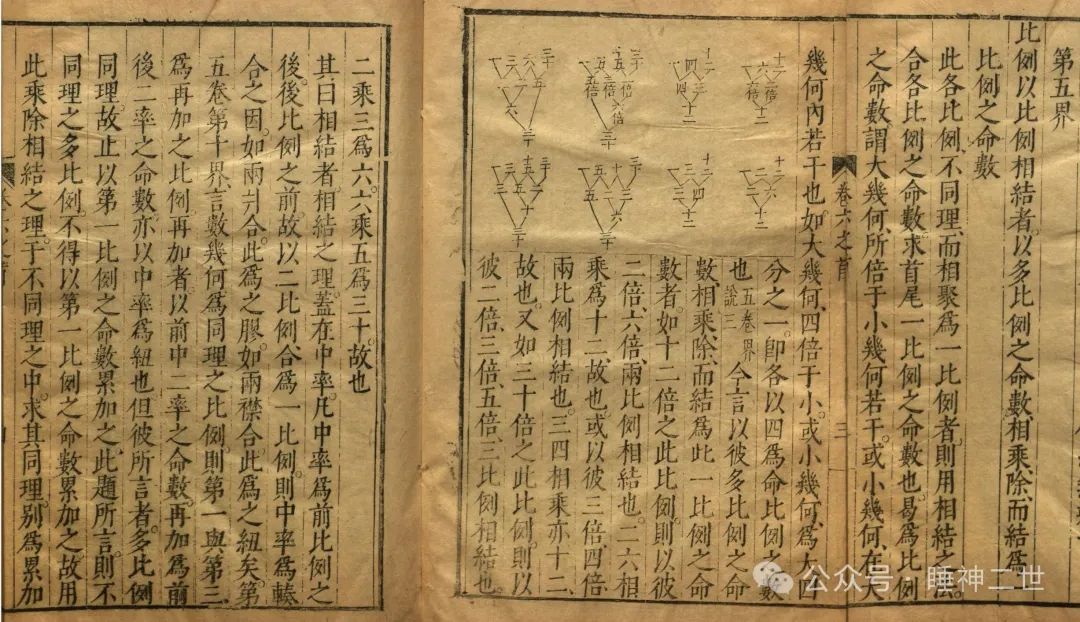
徐版第六卷的界说第五界引入了命数的概念，作者用了10页的篇幅介绍如何用相结之法把多比例命数转换成为一比例之命数。是不是看不懂我在说什么？这是我们在初中几何中不曾学习的内容。这部分内容读起来很困难，我对他的证明方法也非常不理解，23题费了很大力气定义一个线段的长度去表述一条直线，然后通过线段的比例来计算面积比例关系。但是当我再次引入第一卷第四求中度与数的概念，我大概明白了作者的用意。

第五界作者强调了一个概念“中率”。“则中率为辏合之因。如两爿合此为之胶。如两襟合此为之纽矣”。又是一个应用场景衍生的数学概念。如果在没有标准度量衡的情况下，这条线段代表的是一把尺，在存在多比例时，尺的精度就必须要满足几个比例的公约数。比如2、8、6、14这样一组数据，尺的精度至少要达到2才能完成。3、8、6、18这样一组数据，尺的精度至少要达到1。这样各比例数才能都是整数，方便施工时测量。如果不考虑精度问题，就只是数字问题，完全不需要搞这么复杂。

欧版的第五界又消失了。欧洲人比我还菜，完全读不懂这部分内容，索性就删了吧。但是后面漏了马脚，第五界对应的习题23题，欧版保留了。命数的概念删掉了，相结之法也删掉了，题目里突然冒出一个复比的概念，但是整本书中都没有一个复比的定义。西方人之所以说《几何原本》是纯粹的数学之书，恰恰是因为这本书是从中国抄来的而不是产生于实践之中，与实践相关的内容他们理解不了就删掉了。拉丁文版《欧几里得的元素》是被简化的、漏洞百出的学渣笔记。

徐光启说《几何原本》“所关世用”，列举了众多的应用场景。称这本书的好处就在于“題論之首。先標界說。次設公論題論所據。次乃具題。題有本解。有作法。有推論。先之所徵。必後之所恃。十三卷中。五百餘題。一脈貫通。”既有理论又有实践。翻译这部书的目的就是“推明所以然之故”。

而浩尔资曼说“此本为实用者而作。实用者仅知当然已足，不必更示以所以然之理。故凡关于证明之文，概以芟略云云。”欧洲人压根就读不懂徐光启的几何原本，属于抄作业只抄答案，证明过程都舍弃了。这也解释了为什么欧版以及满文七卷版都是简略版的问题。

同样都认为这本书是实用之书，东西方人对其内容的态度却截然相反，那么东西方人到底谁更有科学精神呢？现实版的学霸VS学渣。

补充：六卷版涉及了勾股定理的证明和黄金分割的定义，按照西方伪史的说法这都是古希腊毕达哥拉斯的数学成就，但是在《几何原本》中都没有提到这个人。

第五卷第六界涉及古希腊欧多克索斯的比例理论，也没有提这个人。

看来1607年毕达哥拉斯、欧多克索斯都还没有编出来。