《重学》3：李善兰发明了代数学

重学发展到十九世纪中叶，在中国出现的最重要的一本力学著作就是传教士艾约瑟口译、李善兰笔述的这本《重学》。

十九世纪出版的力学著作都没有超出这本《重学》的范畴，也就是说李善兰的《重学》是19世纪中国力学著作的巅峰。

李善兰在1852年加入墨海书馆后即开始“朝译《几何》，暮译《重学》”，并在1855年完成了《重学》的内容，也就是说《重学》是李善兰加入墨海书馆后完成的第一部著作。（《续几何原本》是1856年完成。）

李善兰完成《重学》的时间是1855年，而今天我们看到的《重学》是刊行于同治五年（1866年）的金陵书局版，这一版本是李善兰独立刊刻的，没有传教士的参与，此时墨海书馆都已经关闭6年了。在此之前还刊刻过一版是在1859年由李善兰的好友顾观光、张文虎校订、钱熙辅出资刊刻的。由于战乱这一版遭到毁坏，今已无存。此后1867年美华书馆又刊印了一版《重学》，根据张文虎日记的记述，“壬叔赠夷人重刊《重学》即据钱升卿(钱熙辅)学博原刊本”，即美华版用的是钱熙辅刊刻的原版。因此在考察两个版本内容时应该注意到美华版的内容实际产生时间更早。

对比金陵版和美华版，可以发现以下信息：

1. 金陵版由李善兰主导刊刻，美华版由传教士主导刊刻。

2. 金陵版包含了重学17卷+流质重学略论3卷+圆锥曲线说3卷。美华版包含重学浅说、重学17卷。

3. 金陵版在表示分数时分子在上分母在下，与现代使用的方式相同。美华版是分母在上分子在下，与现代方法相反。

4.《重学》是中国第一部使用代数方法解决数学问题的著作。

首先可以看出李善兰与艾约瑟对待译书的态度是一样的，可以任意的增加和组合新的内容进来，而不需要考虑原著的内容。这显然不是正常的翻译逻辑，既然是翻译著作当然应该考虑尊重原作的思路和完整性。

晚清另一位著名译者华蘅芳描述他们的翻译工作是这么说的：

“笔述之时须将口译之字一一写出，不可少有脱漏，亦不可稍有增损改易也。至誊出清本之时，则须酌改其文理字句，然所致之字句必须与口译之意极其切当，不可因欲求古雅致，致与西书之意不合也。所译之书若能字字确切，则将华文再译西文，仍可十得八九所以译书之人务得原书之面目，使之惟妙惟肖，而不可略参私意也。”

如果以此为标准李善兰和艾约瑟的行为都是在编书和不是译书。正如《重学》2：伽利略是19世纪传教士编造的中所推测的并不存在一本胡威立的力学著作，胡威立只是托名伪造的。华蘅芳和李善兰至少有一人撒了谎，抑或是都撒了谎。

流质重学略论三卷和圆锥曲线说三卷是李善兰离开墨海书馆后增加的内容，不是与传教士共同完成的，那么只能是李善兰独立完成的。而美华版这一再版也没包含这些内容，也说明这些内容是由李善兰掌控的。

王韬在《弢园文录外编》中说:“是书(《重学浅说》)向编入《六合丛谈》中，亦有单行本，后乃冠于艾约瑟所译重学之首，余与伟君皆未署名。”王韬的说法和美华版的结构是吻合的。《重学浅说》的内容与《重学》是重叠的。前文已经分析过《重学浅说》的知识点都出自《奇器图说》，且没有任何知识点是超越《奇器图说》的。这说明西方人在学习了200多年《奇器图说》后并没有在理论上产生任何突破性的研究。《重学》17卷的内容是结构合理的，而把《重学浅说》置于《重学》的卷首部分，完全没有必要。李善兰主编的金陵版就没有这部分内容。说明传教士对于书中的内容并不理解，只是一味的求多求全。

《重学》与《重学浅说》主要的差别是加入了大量数学运算对具体问题进行分析。而众所周知李善兰是清末杰出的数学家，（他的杰出程度可能超出所有国人的认知，这一部分我会单开一个系列来讲述。）他完全具备使用数学方法对《力艺》重新进行解读并创作出《重学》的能力。

关于分数的表示方式，金陵版与美华版的分数表示方法是颠倒的，恰恰说明此时的分数式处在不成熟的过渡状态，而现代分数的创造者就是李善兰本人。

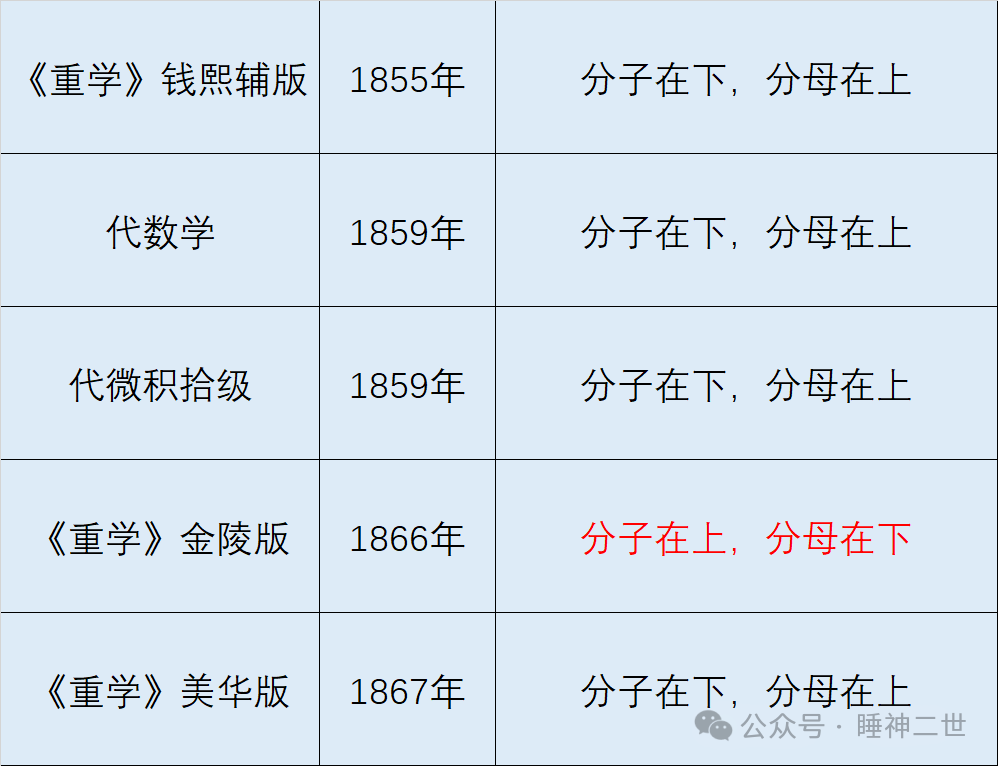
从上表可以看出，墨海书馆时期出版的科技书籍，普遍采用了分子在下分母在上的形式，与今天的分数式相反。《重学》金陵版李善兰具有较高的决定权，可以确定把分子分母倒置的写法是李善兰创造的。此后的分数式都沿用了李善兰金陵版的表示方式，一直传承至今。美华版是钱熙辅版的复刻可以忽略。因此分数表示方法改变的转折点就是李善兰金陵版《重学》。

在此之前中国的分数表示方法都是采用分子在下分母在上，这可以上溯到明末李之藻所编写的《同文算指》，以后200多年一直被沿用，因此在墨海书局的著作中李善兰便沿用了这种方式。李善兰在出版金陵版时改变了这一方式应该是为了与/的记述方式相统一。这恰恰反映出事物逐步发展完善的过程。

李之藻《同文算指》

那么有没有可能西方一直是在用分子在上分母在下的形式，故意给中国人用相反的形式呢？答案是不可能。继续上证据。

这个证据的提供者恰恰是墨海书馆的印工伟烈亚力。伟烈亚力在1853年出版了一本《数学启蒙》，这本书被冠名为伟烈亚力独立完成的。所有的文献资料都把它称为伟烈亚力引进中国的西方代数学知识，是《代数学》的前身。但是看过这本书后我发现这本书就是李之藻《同文算指》、梅瑴成《数理精蕴》的汇编。

伟烈亚力《数学启蒙》

伟烈亚力的英文序言

网上没有找到1853年的版本，只看到1897年的版本。在这一版的英文序言中，伟烈亚力直接承认这部书的内容就是来自于中国学者的《同文算指》、《数理精蕴》和《算法大成》，并且把它称为代数学的入门书籍。可见晚清中国人所学习的数学知识其实都是出自《同文算指》《数理精蕴》这些中国古籍，却在封面上被冠以“西法”。

从目录可以大致了解《数学启蒙》的内容，虽然只是代数入门知识，但已经涉及到对数、开乘方等的各种运算。可是全书居然没有一个＋、-、×、÷符号，而分数也沿用了分子在下分母在上的形式。你能想象一个学习对数知识的高中生还不会使用＋、-、×、÷，是多么的不便吗？

分子在下，分母在上

没有加号，没有等号，没有算术式，全部用文字叙述

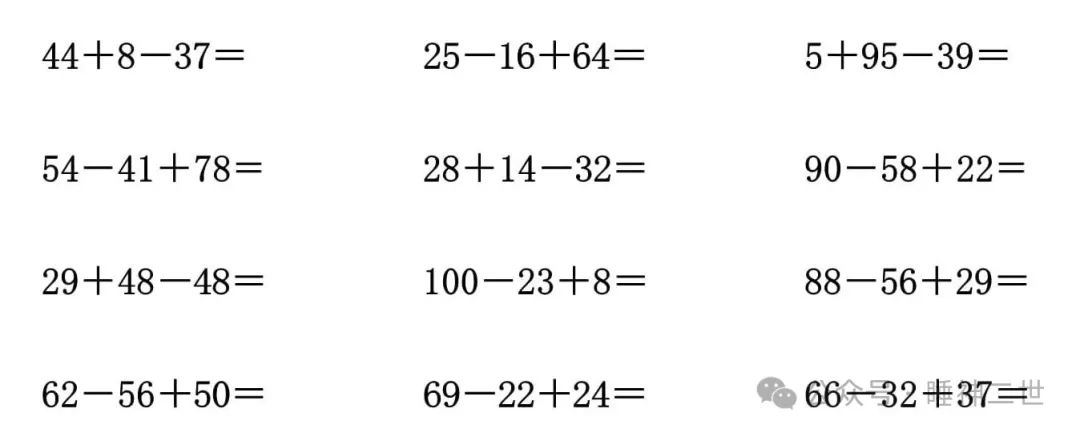
小学生数学题

显而易见我们今天使用的算术式、代数式，其便捷程度远远超过中国古代以文字叙述的方式，传教士自1600年至1853年这250年间所译的全部书籍都宁愿使用一种复杂繁琐、书写量巨大的记述方式，而坚决不使用算术式和代数式。直到1855年李善兰的《重学》开始使用汉字代数式表示物理公式和数学计算。放着便捷的算术式、代数式不用，传教士们吭哧瘪肚的用汉字描述算不算一种自虐倾向？还是单纯的不喜欢呢？

这客观上说明了西方当时并不存在一套独立的代数学体系，也谈不上有另外一种相反的分数记法。

重学中使用的代数运算

李善兰在编写《重学》的过程中发明了一整套代数符号，包括我们今天使用的＋、-、×、÷、=、>、<、分数线、根号等等，以及使用字母（字）表示未知量进行运算的方法，以此建立了代数学。未知量一般用天干（甲乙丙丁）、地支（子丑寅卯）、二十八宿（角亢氐房）以及天、地、人、物来表示，数字用汉字数字表示，如上图。于是才有了《代数学》、《代微积拾级》等著作。

上图中的速度公式可能是世界上最早发表的物理公式。

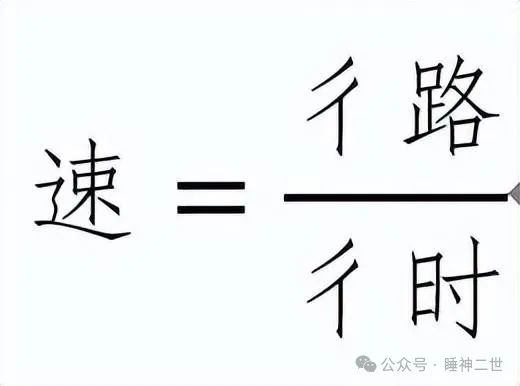
且他是一个微分公式，李善兰此时已经掌握了微分学。

这样的书写方式在今天看来似乎还是太复杂了，而西方人窃取了这些学术成果后用字母来代替反而得到了最便捷的书写模式，又被中国人引进。也恰恰因此“科技来自西方”的印象被进一步加深。

《数学启蒙》出于《同文算指》和《数理精蕴》，没有使用代数式，此后李善兰发表了《代数学》。这一过程与力学著作的发展出奇的一致，《重学浅说》出于《奇器图说》，没有使用代数式，此后李善兰发表《重学》，使用代数方法解决力学问题。转折点便是李善兰加入了墨海书馆。

今日暴论来了，1855年以前西方没有代数学，李善兰的《重学》是人类历史上第一部应用代数方法的著作。因此1855年以前所有使用公式进行计算的推演方式都是后来伪造的，使用过公式或代数进行推理的科学家都是后期托古伪造的。

说回《重学》，重学最核心的内容当然是牛顿三大定律：

“物动速及方向皆以所加之力为准，此理分为三例。”

“动理第一例：凡动无他力加之，则方向必直，迟速必平，无他力加之，则无变方向及迟速之根源故也。”

“动理第二例：有力加于动物上，动物必生新方向及新速，新方向即力方向，新速与力之大小率比例恒同。”

“广动理第三例：凡有抵力，由合质体加他物而生动，动力与抵力比例恒同。”

墨海书馆的著作都会利用一切机会介绍西方科学家的成就，然而运动三定律却只字不提奈端，甚至全书都没有提过一次奈端。反倒是在测算重力加速度时提到了伽利略和阿特伍德，正如我在《重学》2：伽利略是19世纪传教士编造的（补充）中所说，此时的传教士集中精力塑造的物理学家是伽利略，奈端还没到登场的时候。至少在1860年墨海书馆关闭之时，牛顿的形象仍然没有形成。

至此《奇器图说》-《重学》系列就到此结束了，谈谈我的心路历程。在《奇器图说》1：遗落在牛顿头上的那颗苹果发现在明朝末年还只有20个拉丁字母，说明当时的欧洲语言还没有完善。于是我产生了一个想法，使用字母进行代数演算和科学公式是何时开始使用的呢？

在《奇器图说》2：阿基米德原来是“亚·昔·墨翟”发现阿基米德的《论浮体》居然使用几何方法来论证客观规律，用一堆无厘头的假设推演出正确的结论，如同儿戏。使我更为好奇欧洲人何时放弃了几何方法开始使用代数推理呢？

在《重学》2：伽利略是19世纪传教士编造的看了晚清早期的译作后，发现1853年墨海书馆出版的著作仍然没有使用代数式，我开始怀疑完成代数学的是不是李善兰。带着这样的疑问去追溯李善兰的生平履历，简直让我大吃一惊。李善兰被低估的程度将改写人类所有科技史。

在这个过程中我顺带证伪了阿基米德、拉梅利、伽利略和牛顿，而当我理顺了墨海书馆著作的关系后，可以确认李善兰在《重学》的编辑过程中发明了代数学。

而对于李善兰，发明代数只是他学术成就的冰山一角。

李善兰