《永乐大典》里当然没有微积分，微积分是清末李善兰发明的

1852年，41岁的李善兰离开嘉兴来到上海，加入墨海书馆。此时的李善兰已经是著作等身，且学术界公认的数学大家了，而41岁的年龄也是在学术上出成果的黄金期。

在墨海书馆李善兰完成了《几何原本》后九卷、《重学》、《代数学》、《代微积拾级》、《谈天》等大家熟知的著作。这些著作都被冠以传教士口授、李善兰笔录的形式。墨海书馆出版的所有科技类书籍都是在1852年李善兰加入后刊刻的，足以说明李善兰的巨大作用。

关于李善兰加入墨海书馆的原因，推测主要还是出于生计的考虑。由于科举仕途走不通，不得不在嘉兴坐馆教书，而数学成就并不能解决实际的生活问题。墨海书馆的待遇优厚，因此成为一个权宜之计。而加入墨海书馆的代价就是为洋人代笔，把自己的成就都冠名给洋人。比如墨海书馆发行的《六合丛谈》中的文章只有洋人有署名，而王韬编写的所有内容都没有作者。这种现象其实不难理解，知识分子为五斗米折腰，直到今天仍然非常普遍，比如高校的研究生发表研究成果要把第一作者署名给自己的导师，再比如东方某选的小编加班创作文案成就的却是董某辉。在墨海书馆期间李善兰仍然参加过乡试，希望能进入仕途，可惜还是失败了。直到后来他加入了徐有壬的幕僚，才开启了其仕途生涯。

墨海书馆的牛力印刷机

另一个促使李善兰加入墨海书馆的因素是李善兰认为中国战败的原因是造器之术不及西方，加入墨海书馆能够接触到西方的先进技术。但是这一点可能让李善兰失望了，英国人在鸦片战争时使用的军舰是木制帆船，墨海书馆使用的当时最先进的印刷机靠牛的畜力运转，所以英国所谓的工业革命实际的影响有多大目前看是存疑的。从王韬翻译的《重学浅说》来看，西方人此时的科技认知还停留在明末《奇器图说》的水平。从伟烈亚力的《数学启蒙》来看，西方人的数学停留在明代《同文算指》、清中期《数理精蕴》的水平。把这两类著作提升到前所未有高度恰恰是李善兰完成的。

在写《几何原本》系列内容时，我忽略了一个重要信息，李善兰完成后九卷的时间是1856年，于1858年刊刻的初版是由顾观光、张文虎校订、韩应陛出资刊刻的。同样《重学》是1855年完成，在1859年由顾观光、张文虎校订、钱熙辅出资刊刻的。那么问题来了，墨海书馆雇佣过顾观光、张文虎吗？墨海书馆付钱供李善兰完成《重学》和《几何原本》是为了把学术成果免费送给韩应陛和钱熙辅吗？那么墨海书馆雇佣李善兰翻译这两本书目的是什么？

墨海书馆的传教士最初并没有计划出版这些科学书籍，而是想直接窃取后送回西方的，就如同艾约瑟窃取戴煦的《求表捷术》送回英国一样。正是李善兰的不懈努力，在好友们的帮助下才使这些书籍能够刊刻。可见，在墨海书馆的资金支持下能够全身心的完成这些著作应该是李善兰加入墨海书馆的一个重要原因。

在徐光启、利玛窦和《几何原本》（六）、徐光启、利玛窦与《几何原本》（七）中，我论证过《几何原本》后九卷是李善兰根据中国古籍汇编的，其中第十卷应该是李善兰独立创作的，因为这一卷的深度与全书对比之下难度陡然提升，完全不在一个水准。而另一个证据是那个英国人——伟烈亚力。

伟烈亚力（Alexander Wylie，1815-1887年），英国传教士。他在伦敦切尔西的中学学过代数、几何、拉丁语等课程，毕业后当了一名木工，还曾受雇于英国刑事法庭、考文特花园等，并加入了苏格兰长老会。1845年，他读了马若瑟写的《汉文启蒙》，对汉语产生了浓厚兴趣。1846年，伦敦会传教士理雅各返回英国，选拔人才到上海负责墨海书馆的印刷工作。伟烈亚力学习印刷6个月，并向理雅各学习汉语。1847年，伟烈亚力作为印工，被伦敦会派往上海。

伟烈亚力来到上海的身份是一名印工。从伟烈亚力的经历可以看出，他并没有受过深入的数理教育，也没有从事过数学物理方面的研究，充其量是个初中生水平，当他到达中国时最多学了两年中文。对比我在李善兰1：读懂李善兰才能读懂中国古代数学 中分析过的李善兰的数学成就，你能想象这个学了两年中文的印工可以指导李善兰学习代数学、续几何原本、微积分、牛顿三定律、天文历法？并且完美的翻译成中文书籍？伟烈亚力冠名的中文书籍有《数学启蒙》、《重学浅说》、《续几何原本》、《代数学》、《代微积拾级》，而他冠名的英文科技书籍数量为零。

华蘅芳在记述他与玛高温合作翻译时是这么说的：

“惟余于西国文字未能通晓，玛君于中土之学又不其周知，而书中名目之繁、头绪之多，其所记之事迹每离奇恍惚迥出于寻常意计之外，而文理辞句又颠倒重复而不易明，往往观其面色、视其手势，而欲以笔墨达之，岂不难哉!”

是不是与汤若望一个水平（见徐光启、利玛窦与《几何原本》（四））？李善兰不会英语，伟烈亚力这个gai溜子指导李善兰翻译几何原本、牛顿力学和微积分简直是天方夜谭。那么李善兰在墨海书馆的成就只能来自他自己的独创以及中国古籍的汇编。

续几何原本

《几何原本》我用了七篇文章来论述它是一部中国著作，这里就不再赘述了。

重学

《奇器图说》和《重学》我也写了八篇文章分析，同样是发源于中国古代的著作。我做了一个推测，《重学》是李善兰在《奇器图说》的基础上加入了数学推导和计算而完成的。这一推断我也找到了证据。

1867年，美华书馆再版了李善兰的《重学》，在这一版中收入了伟烈亚力的一篇英文序言。序言中先是介绍了《奇器图说》，然后说《奇》的内容已经落后了，将数学应用于理论的发展开辟了新的研究领域，于是有了这本《重学》。这不正是李善兰加入墨海书馆的意义吗？也解释了《重学》的成书过程。伟烈亚力虽然强调这本书翻译自西方胡威立的著作，但讲到成书过程就露馅了。

代数学

在重学系列我还提出了一个观点，李善兰发明了代数学。在1859年李善兰编写的《代数学》刊刻以前西方都没有代数式，没有函数，没有使用字母表示未知量的方式，甚至没有+、-、×、÷。详见《重学》3：李善兰发明了代数学 和李善兰1：读懂李善兰才能读懂中国古代数学。

有些网友觉得匪夷所思、过于离谱。别急，我还真找到了证据来证明。

我找到一本1875年美国人关于蒸汽机的科技著作，CATECHISM OF THE LOCOMOTIVE。这本书系统的介绍了蒸汽机的原理和应用。

这两张配图来自1886年的版本

在他的前言中重点介绍了+、-、×、÷的用法。

下面是微信翻译的中文内容，方便大家参考：

你能想象一本600多页的系统介绍蒸汽机车的科技书籍，需要首先从+、-、×、÷的用法开始讲起吗？这并不是一本儿童启蒙读物，而是一部前沿科技的系统教程。显然这种表述方式是此前没有的，所以才要在前言中做解说，此前西方人使用的方法与中国人古籍中的方式是一样的，用语言叙述。

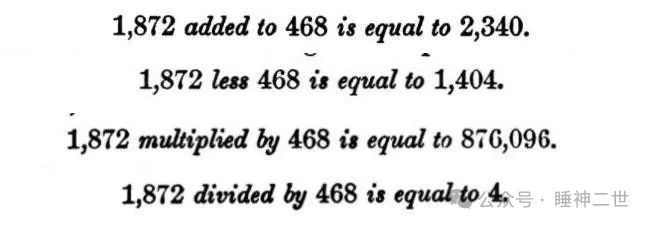
笔算式中也没有+、-、×、÷，这和明清两代所用的方法一样。此时的西方只有《数学启蒙》中的笔算形式，跟中国一样。并没有代数多项式的表达方式。

下图箭头标注的是除法运算，反括号左侧是除数，中间是被除数，右侧是商。这种表示方法在《蒸汽机教程》和伟烈亚力的《数学启蒙》中是相同的。说明1875年的美国所掌握的数学知识与1853年的《数学启蒙》是相当的，他们正在学习1859年李善兰所创造的代数知识。在1859年以前，西方人口中的代数学就是《同文算指》、《数理精蕴》、《数学启蒙》，并不是李善兰《代数学》中体现的内容。

上一篇文章介绍过，李善兰在《四元解》研究的四元术，在《垛积比类》中使用的垛积术和数表，《方圆阐幽》中使用的尖锥术，都是受限于没有代数而采用的方法。此时的李善兰亟需一种简单便捷的方法来描述这些数学问题，于是在《四元解》中做了尝试，在《重学》中做了实践，最终在《代数学》定型。

华蘅芳在《学算笔谈》提到：“秋纫谓余曰：此《代数学》为算学中上乘功夫，此书一出，非特中法几可尽费，即西法之古者，亦无所用之矣。”

李善兰告诉华蘅芳，代数学一出，不但中国古代的数学方法全没用了，西方古代的数学方法也没用了，这不就是直白的告诉大家，代数学是李善兰独创的。

至此，李善兰发明了代数学可以确证。

华蘅芳在学习了《代数学》后，也编写了一本代数学著作《代数术》。其思想来源于李善兰而不是传教士，这一过程是非常明确的。

代微积拾级

在《代数学》发行同年，李善兰还刊刻了另一部数学著作《代微积拾（shè）级》。《代微积拾级》延续《代数学》的内容，讨论了代数几何、微分、积分三部分内容。当代把代数几何称为解析几何，研究代数式如何转换为直角坐标系中的几何图形来表示。但按照我们的思路，是先有几何学再有代数学，此时李善兰研究的是如何使用刚刚发明的代数方法来表达几何图形，所以书名用代数几何才是最合理的。

在英文序言之后，伟烈亚力非常贴心的附上了中英文术语对照表。这种在前言附上术语对照表的习惯都出现于西方传教士主持出版的刊物上，比如墨海版《代微积拾级》、美华版《重学》、墨海版《谈天》等。而李善兰主持出版的书籍比如金陵版《重学》、十五卷《几何原本》以及江南制造局版《谈天》则没有。一方面说明李善兰及中国译者对于中英文术语对照并不在意，这些内容本就是李善兰原创。另一方面说明中英对照对于传教士很重要，西方的表音文字需要中文的表意来固定这些单词。

我在小学学习未知数时曾有一个疑问，为什么设未知数都是使用x、y、z、w？而不是用a、b、c、d或者o、p、q、r？为什么w排在z后面，u、v怎么不用？没有想到几十年后我居然找到了答案。

上图红框内，给定了w、x、y、z与物、天、地、人的对应关系，而李善兰遵循中国古代的天元术、四元术的习惯，首设未知量肯定是用天元，其次就按照天、地、人、物的顺序来。传教士照抄回去自然就变成了x、y、z、w。西方没有四元术，不会受到四个未知数数量的限制，为什么会形成四个未知量的设定习惯？这是西方数学无法隐藏的中国基因。

伟烈亚力在序中说牛顿与莱布尼茨同时创造了微积分，牛顿用的流数法不方便，所以就按照莱布尼茨的方法，用“彳”表示微分，用“禾”表示积分。很多同志都已经分析过了，“彳”是微的部首，“禾”是积的部首，这怎么可能是莱布尼茨设计的？莱布尼茨用中文研究微积分的？微积分符号显然是李善兰发明的，由于这两个符号太明显了，传教士不得不进行了改造。

禾的草书简化为了∫，但它并不是一个字母，也不是英语音标里的那个[ʃ]，而是拉长的S。（我用键盘打字，输入法对这两个字符也是区分对待的。）∫是一个被强行造出来的符号，以至于至今∫都没有一个发音，只能念做Integral（积分）。而彳的草书近似于丁，对应的就是d。这样就解释了为何积分要用一个华丽丽的拉长的S，微分却是这么朴实无华的d。这是微积分中的中国基因。

从研究的内容来看，《方圆阐幽》、《垛积比类》、《对数探源》等内容与《代数学》、《代微积拾级》讨论的问题并不存在代差，从尖锥术进化到解析几何、微积分仅仅只是使用了一种新的表达形式。并不是人们想象中的中国数学从古老的童蒙算术直接飞跃到高等数学。而这种表达形式又是李善兰本人创造的，所以《代微积拾级》毫无疑问是李善兰本人编写的。李善兰独创的尖锥术加上李善兰独创的代数学，就得到了现代的解析几何和微积分。

《代微积拾级》发行后掀起了知识分子学习微积分的热潮：

——仅仅三年后夏鸾翔就完成了使用微积分方法的数学著作《万象一元》，对开高次方、对数、二次曲线等给出 130 多个公式。

——晚清开办的学堂都把《代微积拾级》作为微积分教材。

——华蘅芳在理解了《代微积拾级》后完成了著作《微积溯源》。

——长沙求实书院教习许奎垣利用积分与垛积术之间的关系以及极限工具获得了一、二次幂函数的定积分公式。

——蒋士栋著《微积释马》。

——林传甲对微积分的研究成果编入《微积集证》、《代微积浅释》。

——徐异著有《积分难题》，解决了若干一、二阶常微分方程。

——粤东凌步芳著《微分详说》三卷、《积分详说》四卷。

——澄江南菁高等学堂的教习陈志坚著有《微积阐详》。

微积分在发表之后很快就进入了不断迭代完善的进程中，中国的知识分子们孜孜不断的在积累和发展这个新学科。

1862年，日本的中牟田仓之助来华时购去一批数学著作，其中包括《重学浅说》、《代微积拾级》、《谈天》。高杉晋作买到了《数学启蒙》、《代数学》。日本数学史家三上义夫曾指出：19 世纪 60 年代日本数学家“能读到的最好的微积分书籍只有 Loomis的微积分著作的中译本”。日本最早的数学学会——东京数学会社的两位创始人神田孝平和柳楢悦最初都是通过学习《代微级拾级》掌握了微积分。在日本东北大学藏有神田孝平抄写的汉文《代微级拾级》写本。罗密士的英文版原书传入日本后，学习西算者在学习原书时往往也要参考中文译本。

1872年，东京开成学校（现东京大学）使用的数学教材包括中文版《代数学》、《代微积拾级》、《几何原本》、《数学启蒙》。今天日本人把西方传入的科技知识称为“兰学”，并解释为荷兰人传入的西方科学。兰学为日本奠定了早期的科学根基，使日本自1854年开国后迅速成功地推行近代化。然而荷兰人既没有给日本输入过15卷《几何原本》，也没有输入过代数学和微积分，还需要日本人到中国来引进中译本。这位日本最重要的启蒙思想家神田孝平原本是一位汉学家，却摇身一变成为了兰学家，而兰学家们学习的教材都出自李善兰。显然兰学并不是荷兰学，而是善兰学。

晚清公派了大量留学生去日本学习，谁能想到学到的知识都出自李善兰。而李善兰又多了一个头衔——兰学创始人。