《奇器图说》2：阿基米德原来是“亚·昔·墨翟”

西方人伪造出阿基米德这个物理学的老祖宗，其原型只能是“亚·昔·墨翟”。

继续读《奇器图说》，我们逐条来分析。

第5款涉及了密度的概念，称为“本重”，即“体段一样，而金重银轻，是金之质原本重于银也”。

第29、30款进一步说明了两个物体物质相同，密度也相同；同一物质，其重量与体积成正比。

第38款提到了咸水的密度比纯水的密度大。“水之咸者则其体征为重耳”。唐代段成式《酉阳杂俎》“石莲入水必沉唯盐咸卤能浮之。”北宋赞宁《物类·相感志》“盐卤好煮以石莲投之则浮。”姚宽《西溪从语》“日以莲子试卤，择莲子重者用之。卤浮三莲、四莲，味重，五莲尤重。……”中国古代用石莲测定盐水密度的应用非常广泛。

第39款已知水的重量求其体积。使用了三率法，而三率法就是《九章算术》中的今有术。实际已经包含了ρ=m/V的密度公式。

第40款以后开始讨论浮力问题，即阿基米德定律：浸入静止流体中的物体受到一个浮力，其大小等于该物体所排开的流体重量，其方向竖直向上并通过所排开流体的形心。

西方伪史把密度和浮力的发现和计算都安在了阿基米德头上，先不讨论阿基米德的真实性，我们看看中国古代关于密度的理解和应用：

《淮南子》：“古人见款木浮而知为舟。”《易·系辞下》：“伏羲氏刳木为舟剡木为楫。”舟船的使用就是密度概念的早期应用。

《孟子》：“金重于羽者岂谓一钩金与一舆羽之谓哉?”金比羽毛重（是指在同体积的情况下），而不是一钩金与一车羽毛相比。

《墨经》“经五七：荆之大，其沈浅也，说在具。经说：荆沈，荆之有也。则沈浅非荆浅也。若易五之一。”荆木虽大下沉的却很浅，达到了平衡。荆木下沉的深度就是这个平衡，下沉深度与荆木深度差1/5。即荆木的密度是水的0.8倍。早在“亚·昔·墨翟”之前墨子对浮力和密度都有了准确的认知。

《考工记》:“栗氏为量,改煎金锡则不耗，不耗然后权之，权之然后准之，准之然后量之。”意思是栗氏制造量器,要反复冶炼铜锡合金(青铜)直至精纯，然后测量重量和体积，看是否符合量器的标准。准之的意思就是“以金入水，度金之体积”。这比阿基米德用水测量黄金王冠的纯度早200年。

《孟子》《墨经》《考工记》的记载说明在春秋战国时期，中国人对密度和浮力的认识和应用已经非常广泛了。

《汉书·食货志》“太公为周立九府圜法，黄金方寸，而重一斤”周朝度量衡的标准是以黄金为标准的，一方寸黄金重量为一斤。

《孙子算经》“每方寸物之重为：金一斤，银一十四两，玉一十二两，铜七两半，铅九两半，铁六两，石三两。”在公元三世纪中国人对于不同物质的密度测算已经是非常细致的。

现代公制单位下水的密度是1kg/L，之所以是整数是因为公制单位就是以水的密度为基准的，即4℃下1立方分米纯水的质量为1kg。而《奇器图说》中恰恰就是以水的密度作为基准来考量的，水重是“一尺立方容水六十五斤”，再根据其他物质与水重的比值来计算重力、浮力、密度等。这与“黄金方寸，而重一斤”的思想一脉相承，公制单位是按照中国古代度量单位演化而来的，其制定规则和逻辑都遵循了中国度量衡的标准。

公制单位最早是1795年在法国实施的，并在十九世纪上半叶推广到欧洲其他国家。邓玉函在意大利和伽利略一同学习工作，不知道1627年意大利的重量单位是什么？1687年的牛顿又是用什么重量单位？盎司？磅？盎司既是重量单位又是体积单位，显然欧洲人对于度量根本没有准确的认识。如果重学产生于古希腊，那么为什么公制单位与远隔万里的中国制定的度量标准更接近？

1867年，法国举办了一场有关货币、重量和测量系统的国际会议，这是公制单位的第一次推广应用。也就是说公元前221年秦始皇完成的统一度量衡，欧洲是在1867年才完成的。

在《奇器图说》中还没有产生质量的概念，所谓的重是涵盖了质量、力的概念表述，因此度量单位都是“斤”。我记得在学校学习物理时，老师会反复强调质量、重力的区别，学生也很容易搞混。实际上这就是我们中国人潜移默化的思维方式导致的，重力这个定义在日常生活中是可以忽略的，因为在地球上g=9.8牛/千克是被视为恒定的，那么重力9.8牛顿完全可以用1“公斤力”来表示，既体现了质量又体现了力。因此《奇器图说》使用斤为单位是完全合理的。

如果1牛顿=1kg·m/s²，而千克、米、秒这些单位都产生于1795年以后，那么请问伽利略、牛顿、胡克是如何研究力学的？使用的又是什么单位呢？

据青华道人考证，《奇器图说》的浮力部分内容与阿基米德《论浮体》内容基本一致，认为《论浮体》就是根据《奇器图说》编成的。于是我就去看了阿基米德的《论浮体》，真的是不看不知道，一看吓一跳。

《论浮体》的结构显然是在模仿《几何原本》，开篇就是一个公设，接下来引出各个命题。但是这个公设1居然是一个假说，在没有任何定义的情况下，就提出了对流体特征的假设。“他的各部分处于平滑均匀和连续状态，受到推力较小的部分会被受到推力较大的部分所推动”，这样一个复杂描述居然是这本书的最基本框架，而这个描述没有任何的推理过程，也没有任何实验数据。真是天降大神。

“如果流体被渗入任何物体并受到任何其他物体的压缩，那么流体的各部分将受到在它上面的流体的垂直方向的推力”。这就不对了，液体被压缩，这个压缩的力方向没有给定，为什么流体受到的是垂直方向的推力？如果液体仍保持在这个物体内，也就是液体保持静止，那么作用力与反作用力相抵消，也不能说它受到垂直方向的推力，结论也不成立。

公设1看的糊里糊涂的，那就再看看命题吧。命题3就是物体与液体密度相等，物体会悬浮在液体中。对应了《奇器图说》的第40款。令人吃惊的是阿基米德居然是用几何方法来论证物理问题的。

1.先做一个地球的模型，O点为地心。等等，古希腊时代就已经确定地球是圆的了？在没有大航海能力，没有观测技术，连浮力还没有搞清楚前就确立地球是圆的，然后以此为基础来论证浮体的特性，阿基米德这明显是使用了时光机啊。

2.看了这个证明过程，我大概理解公设1想表达的意思了。阿基米德认为把物体放入水中，会给水的底部造成压力，因此PQ的压力比QR大，水继续流动，直到物体悬浮才能达到平衡。今天我们知道水的压强只与水的深度有关，因此无论EGHF在哪个位置，PQ与QR的压力都是相同的，这个命题的证明完全是错的。

3.印象中我们在学习物理的过程中，只有力的合成、分解，运动的合成、分解，光的折射这些问题会用到几何方法。大部分的学习过程都是理论+实验，用实践去验证理论的真实性。何曾用过几何方法去验证的？使用几何方法推理完全就是不合理的，因为几何构建的模型根本无法模拟客观世界存在的规律，如何验证几何模型与客观世界是相同的？这完全就是一种臆测和想象。

公设是错的，假设条件是不确定的，论证过程是错误的，论证方法是不合理的，然后得出一个完美的结论。再一次佩服阿基米德真是天降大神。

评论里总有人说《几何原本》开创了公理化的方法，这是中国人所没有的。那你们看看这就是阿基米德的公理化水平，这有什么好吹的呢？联想到牛顿的《自然哲学的数学原理》使用的也都是几何方法来论证物理问题，我开始明白《几何原本》为什么这么重要了。因为西方所有科学的基础都是以几何推导来完成了，失去了《几何原本》的著作权，西方文明的根基就崩塌了。我以前认为《几何原本》是西方科学的根基只是一个比喻，西方不是还有其他学科吗，没想到其他学科都是直接拿几何学搭出来的。这就尴尬喽~

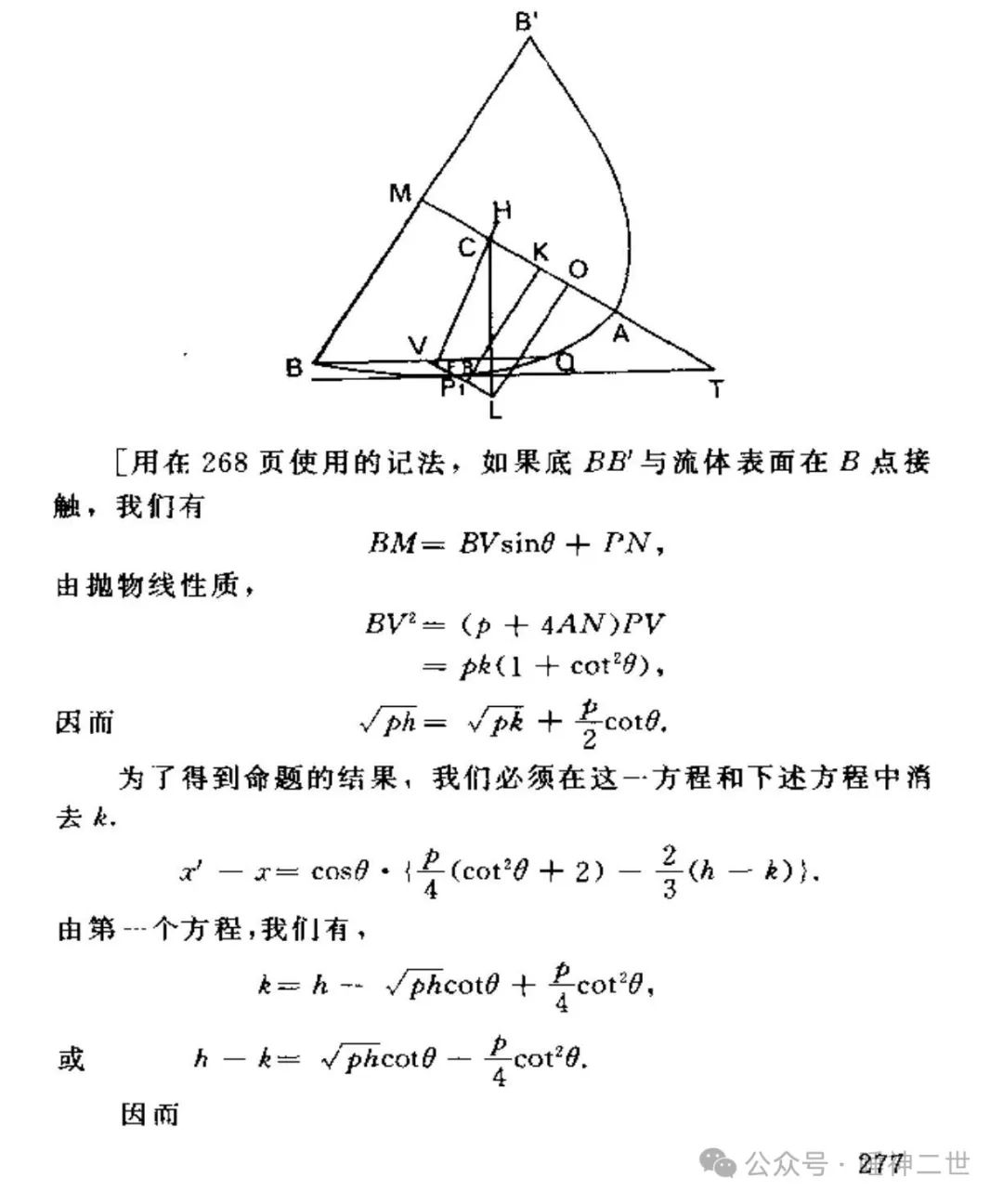
论浮体第二卷开始讨论了复杂的抛物面体，使用了复杂的三角函数和数学公式，这就像西方考古一样一眼假了。至少在明末清初西方还没有产生现代我们常用的数学公式，《几何原本》《奇器图说》还在使用中国传统的三率法，牛顿的《自然哲学的数学原理》（1687年）中也没有。最早的数学公式出现在1859年李善兰所编写的《代数学》。古希腊人根本不可能完成这么复杂的数学计算。

更关键的问题是古希腊没有十进制。据说古希腊使用古希腊字母表示数字，使用方法与后来的罗马数字相似。罗马数字1、2、3、4、5分别是I、II、III、IV、V，10是X，50是L，100是C，500是D，1000是M。1683用罗马数字表示是MDCLXXXIII，用堆叠法把一堆数字放一块。这样的数字连乘除法都做不了，怎么发展出上图中这些复杂运算的？

《奇器图说》第一卷讨论了重学的理论，涉及了地心引力、密度、重心、浮力的原理和关系。其理论与明代实际生产力水平是相符的，前后连贯自成一体。而《论浮体》中或是由臆想得出的结论，或是远远超出实际科技水平，明显是后人杜撰的。

这里提一个推测，西方所有以几何学为论证方式的物理著作，都是后来伪造的。也就是明末传教士偷走的科技知识，以《几何原本》为基础，西方人错误的认为几何学是一切科学的基础，因此妄图用几何学去论证其他科技理论，比如《奇器图说》中的重学。因此导致他们很多理论都是臆想的、错误的，不得不在清初和清末再次来中国重新获取最新的科技成果。

西方人伪造出阿基米德这个物理学的老祖宗，其原型只能是“亚·昔·墨翟”。