读懂李善兰，才能读懂中国古代数学

李善兰的学术成就要论述的内容太多了，必须要单开一个系列才能说清楚。

李善兰

李善兰（1811-1882年），原名李心兰，字竟芳，号秋纫，别号壬叔，浙江海宁人。李善兰10岁开始学习《九章算术》，15岁读了徐光启的《几何原本》。14岁就中了秀才，但乡试失败。在杭州乡试时碰巧买到了李冶的《测圆海镜》和戴震的《勾股割圆记》。

《测圆海镜》是一部用天元术讨论几何问题的专著。而戴震则是一位重要的持“西学中源”思想的数学家，《勾股割圆记》所研究的割圆八线（三角函数）也是传统数学研究的重要内容。这两本书对年轻的李善兰影响非常深远。

1835年，金山钱氏要刊刻一套《守山阁丛书》，钱熙祚及其堂弟钱熙泰邀请顾观光、张文虎、李善兰等人到西湖文澜阁观《四库全书》，“居两月,校书八十余种,抄书四百三十二卷”。其中算学书籍包括《数学补论》、《岁实消长辨》、《恒气注历辨》、《中西合法拟草》、《算腾》、《正弧三角疏论》、《开元占经》等。这一年，李善兰24岁。

金山钱氏以刊书闻名，钱熙祚、钱熙辅、钱熙泰都是知名的藏书家，钱氏聘用顾观光、张文虎校书。顾观光也是著名的数学家，自幼就常去藏书颇丰的钱熙祚家里借读。李善兰能够参与到《守山阁丛书》的校订工作中，大概也是受雇于钱氏。在此期间李善兰从钱氏的藏书中大获裨益，仅《守山阁丛书》中收录的就有苏颂《新仪象法要》、熊三拔《简平仪说》、李之藻《浑盖通宪图说》、《圜容较义》、王锡阐《晓庵新法》、《五经行度解》、薛凤祚《天步真原》、王征《奇器图说》等。李善兰说自己“善兰自束发学算，三十后所造渐深。”足见这一时期对李善兰成就的影响。这一时期的交往使李善兰与顾观光、张文虎成为了一生的挚友。

1845年，为了生计34岁的李善兰来到嘉兴，在陆费家坐馆教书。在嘉兴李善兰完成了《四元解》、《垛积比类》、《方圆阐幽》、《弧矢启秘》、《对数探源》、《麟德术解》等多部数学著作。与戴煦、张文虎、徐有壬、汪曰桢、张福僖等数学家都有密切的交流。

以下的内容可能比较催眠，涉及到这些著作的具体内容。虽然有点枯燥，但我觉得有必要具体分析一下李善兰此时所研究的数学问题，对于我们了解中国数学历史和李善兰的成就是必要的。

大学里有棵树，上面挂满了学生，这棵树的名字，叫作高数。相信很多大学生对这句话都很熟悉，高等数学是很多大一新生的噩梦。而讨论李善兰就离不开高等数学中所涉及的内容。如果你看不懂今天的内容，不用怀疑，那就是我没讲明白。可以直接划到文末看结论。

《四元解》

在介绍《四元解》前先要简述一下中国古代的方程问题，经历了方程术、天元术、二、三、四元术等多个阶段。

早在汉代《九章算术》中就出现了方程术，专门讨论如何建立多元一次方程组求解未知数的方法。

“程，课程也。群物总杂，各列有数，总言其实。令每行为率。二物者再程，三物者三程，皆如物数程之。并列为行，故谓之方程。行之左右无所同存，且为有所据而言耳。此都术也，以空言难晓，故特系之禾以决之。又列中、左行如右行也。”

方者，有行有列是为方。程者，课程、程序也。方程就是按照一定程序列出的方形，用来求数的方法。

以第一题为例，看看方程术是如何求解的。

“今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗。问上、中、下禾实一秉各几何？”

今天我们做这道题很简单，设上禾为x，中禾为y，下禾为z，那么

3x+2y+z=39

2x+3y+z=34

x+2y+3z=26

解这个三元一次方程组就可以算出未知数的值。

九章算术方程术的方法是以筹算的数值列方程，如下图

虽然没有出现未知量x、y、z，但已经具备了方程组的所有功能。使用通分和加减多项式来消元，就可以求得结果：上禾一秉九斗四分斗之一。中禾一秉四斗四分斗之一。下禾一秉二斗四分斗之三。

方程术在金元时期的《测圆海镜》演变为天元术。所谓“天元术”,就是设一个未知数为天元一（即x）。如下图，元表示未知数的一次项，下方是常数项，上方依次是未知数的高次项，仍然是以筹算方式记数研究一元多次方程

这就是用中国的天元术表示的数学公式：

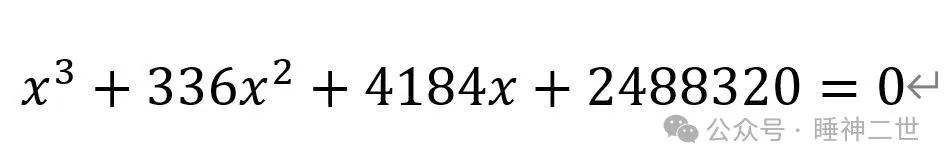
在《测圆海镜》之后出现了二元术、三元术，直到元代数学家朱世杰的《四元玉鉴》发展为四元术，讨论四个未知量，即天元、地元、人元、物元（即x，y，z，w）。清末数学家徐有壬、戴煦、罗士琳都有对《四元玉鉴》的研究著作。李善兰研究《四元玉鉴》是因为汪曰桢向其请教，称《四元玉鉴》全书288问只有4问给出了算式，且都没有计算过程，李善兰“深思七昼夜，尽通其法，乃解明之”，并把他的研究编成了《四元解》。

四元术中，用“太”表示常数项，如图太下方为天元，左侧是地元，右侧是人元，上方是物元，相当于未知量x、y、z、w。

图中表示的多项式就是x+y+z+w。如果要求（x+y+z+w）²，可以代入展开，即为

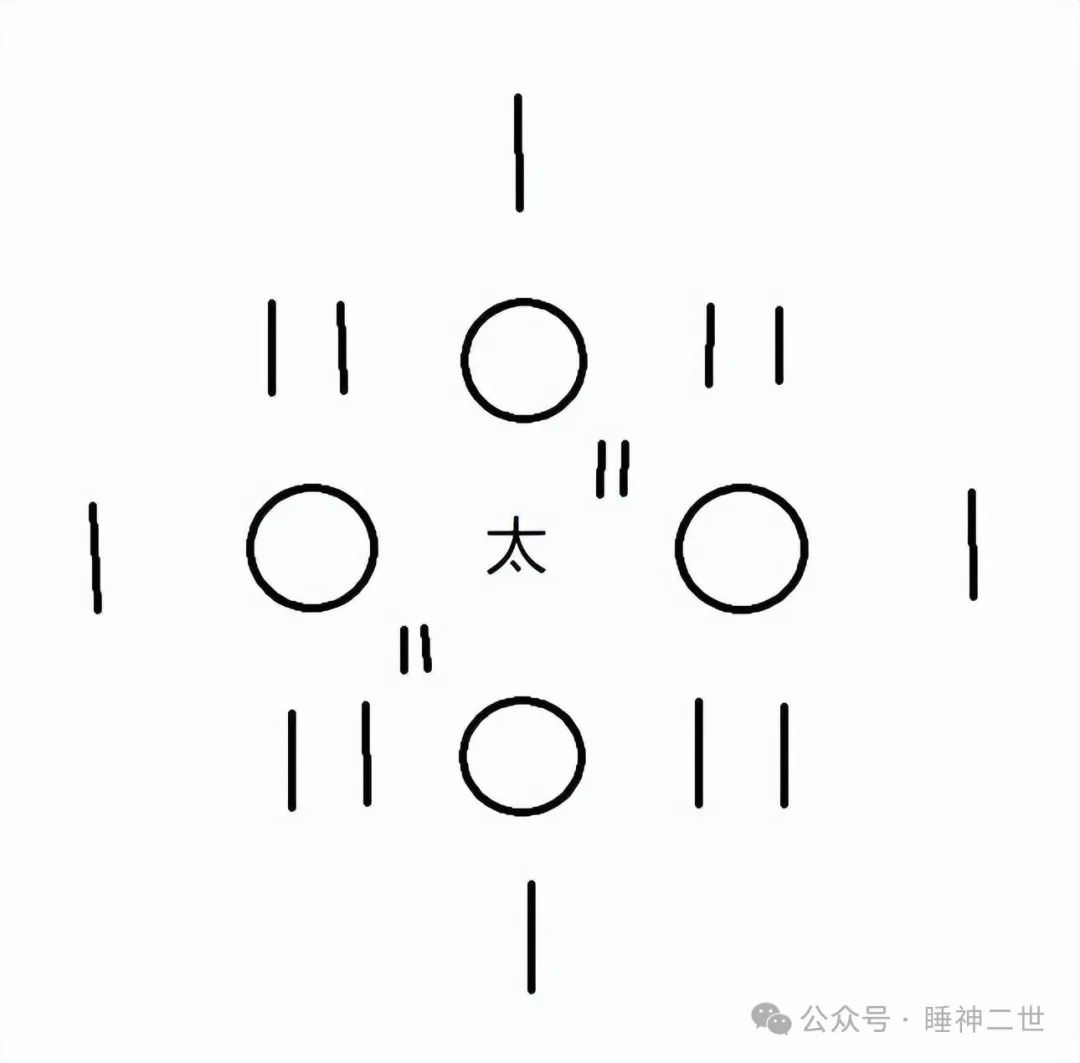
每向外一层代表未知量的指数+1，这个公式用今天的方法表示就是

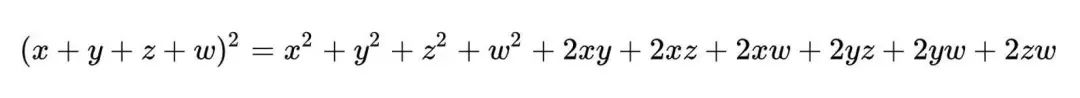
这种方式我们今天理解起来确实很困难，在天元地元夹缝中还有记数，也非常容易出错。

李善兰在《四元解》中使用了新的方法，更直观的表述了未知量的n次方。

这应该是中国历史上第一次使用“天”“地”“人”“物”作为代数符号来表示未知量，并对未知量进行代数运算。就是我们今天所使用的x²，即x²y。

这一年李善兰34岁，距离他加入墨海书馆还有7年，此时他已经在摸索如何使用代数符号的问题了。人类不会凭空发明出一门学科叫代数学，而是有具体面临的问题才会去想解决办法。正是由于四元术在表现方式上受限，才激发了李善兰发明代数法的动机。而远隔欧亚大陆，李善兰发明的示数方法竟然与西方数学方法完全对应，会有这样的巧合吗？

《四元解》中的代数表示方法是李善兰发明代数学的又一证据，再次证明了我上一篇文章的观点。

《四元解》—《重学》—《代数学》，对应了李善兰发明代数学的全过程，即：摸索—实践—定型。（参考：《重学》3：李善兰发明了代数学）

《垛积比类》

垛积术是中国传统的数学方法，最早见于北宋科学家沈括的《梦溪笔谈》，研究的是瓦罐、草垛、砖石筑坝等堆垛的数量问题，逐渐深入为讨论数列求和（级数）的问题。

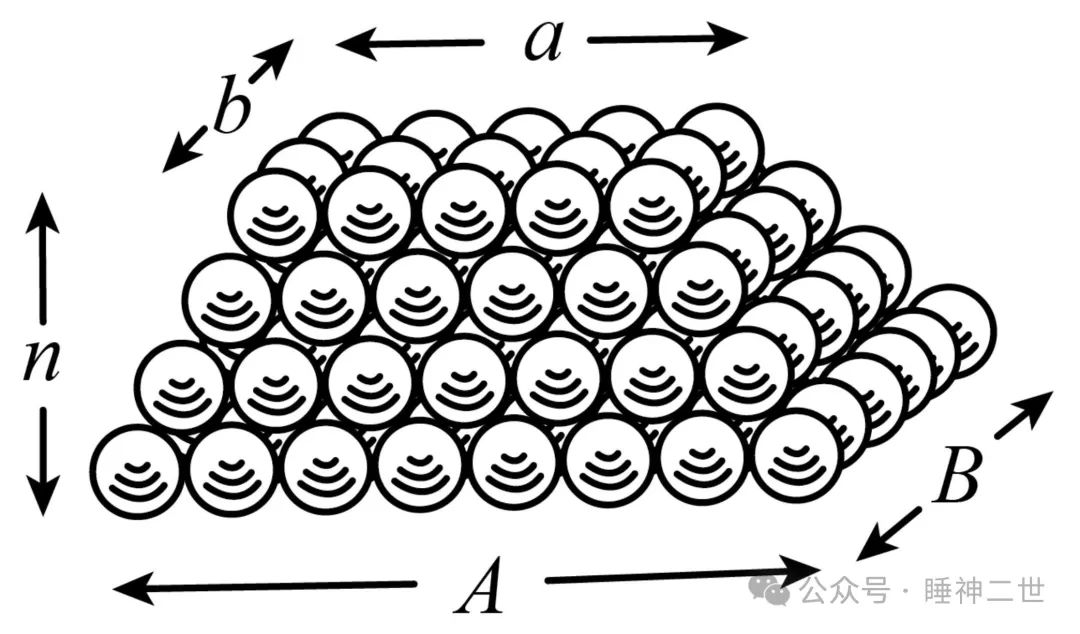
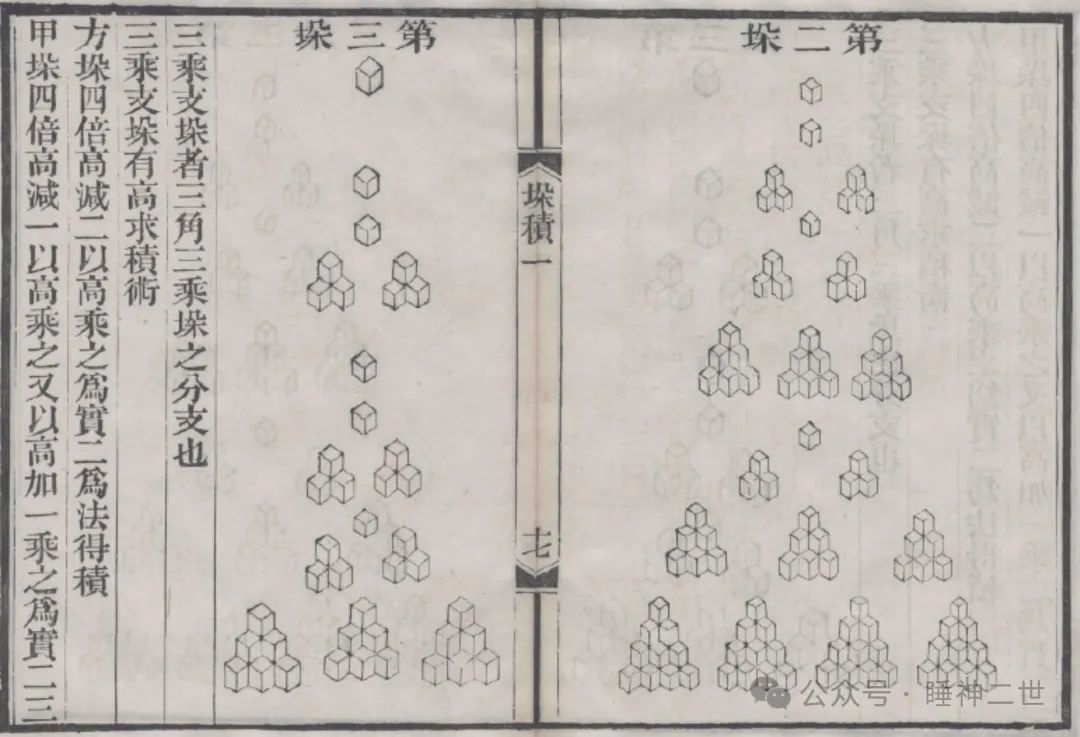
在沈括之后，南宋杨辉的《详解九章算法》、元代朱世杰的《四元玉鉴》继续深入讨论了多种高阶等差数列的求和方法。李善兰继承了杨辉和朱世杰的数学思想，完成了这部高阶等差级数和组合函数的巅峰著作《垛积比类》。

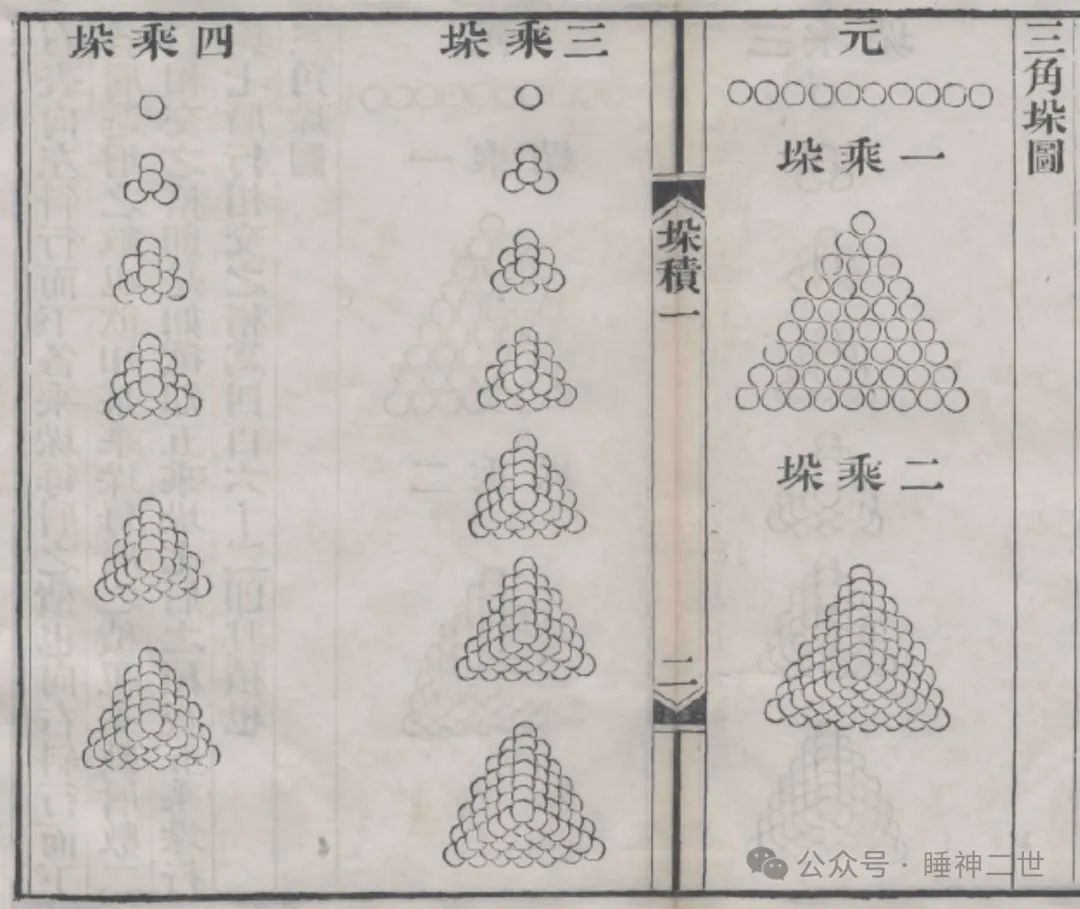
从图上可以看出，垛积术是中国人在没有代数表达式的情况下发明的研究高阶数列级数的表达方法，不同的堆垛形式代表了不同的数列组合形式。

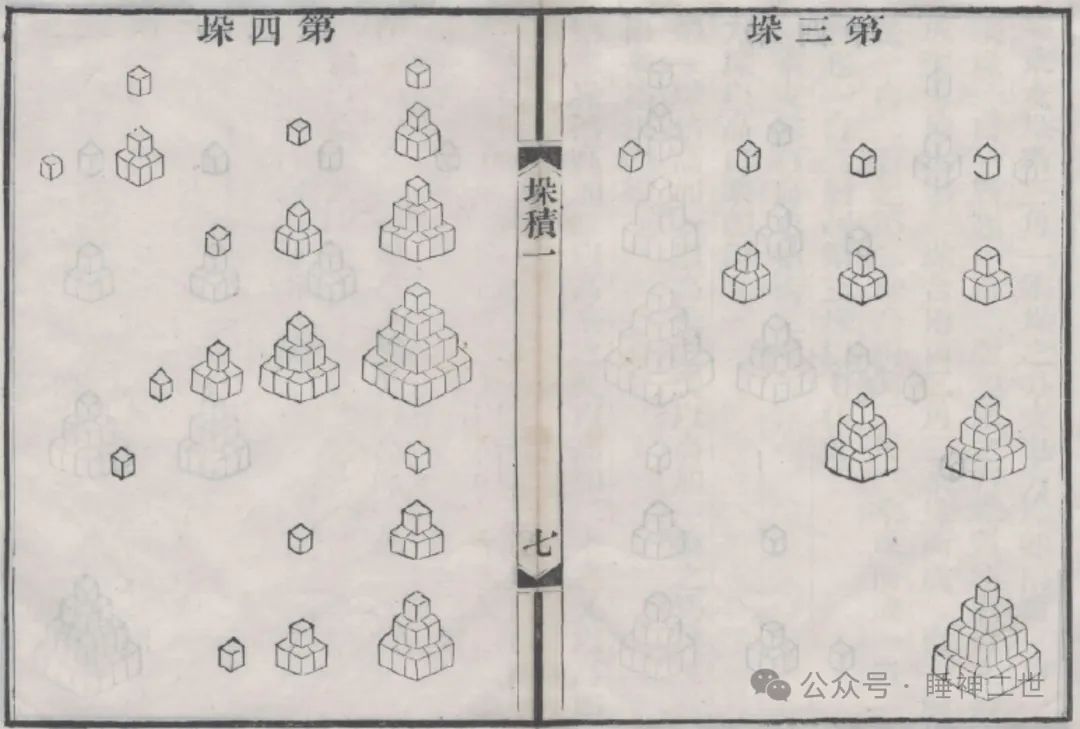
对于不同的堆垛形式，李善兰一一给出了求解方法和系数表，说明李善兰虽然没有代数式但已经掌握了这些递归函数的规律。在这些表中除了三角垛是沿用了贾宪三角（又称杨辉三角，即二项式系数表），“三角有高开方廉隅表”中体现了“第一、第二类司脱林数的绝对值表”，“乘方各廉表”体现了“欧拉数”，卷三“三角自乘垛表”被称为“李善兰恒等式”，卷四涉及了“李善兰多项式”和“费马恒等式”。这些都是李善兰独立完成的。

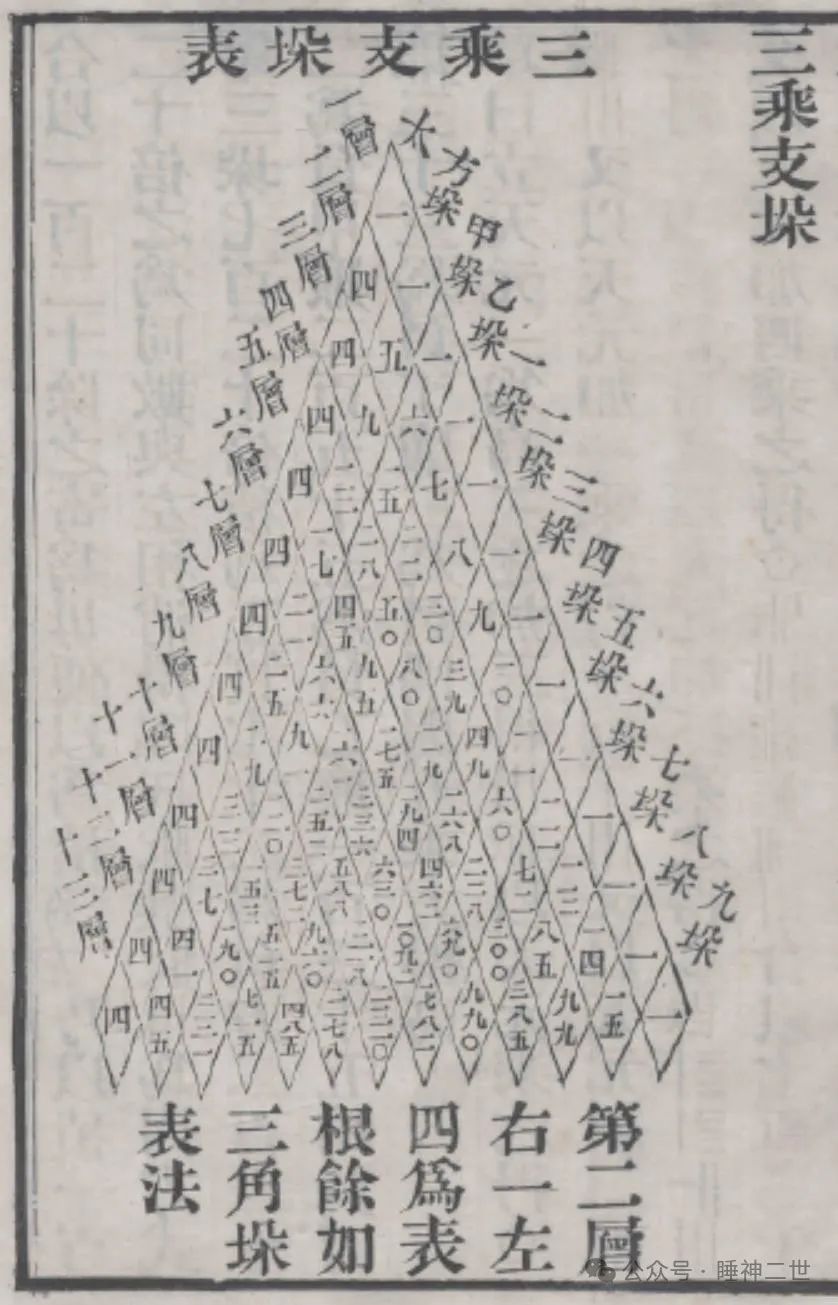
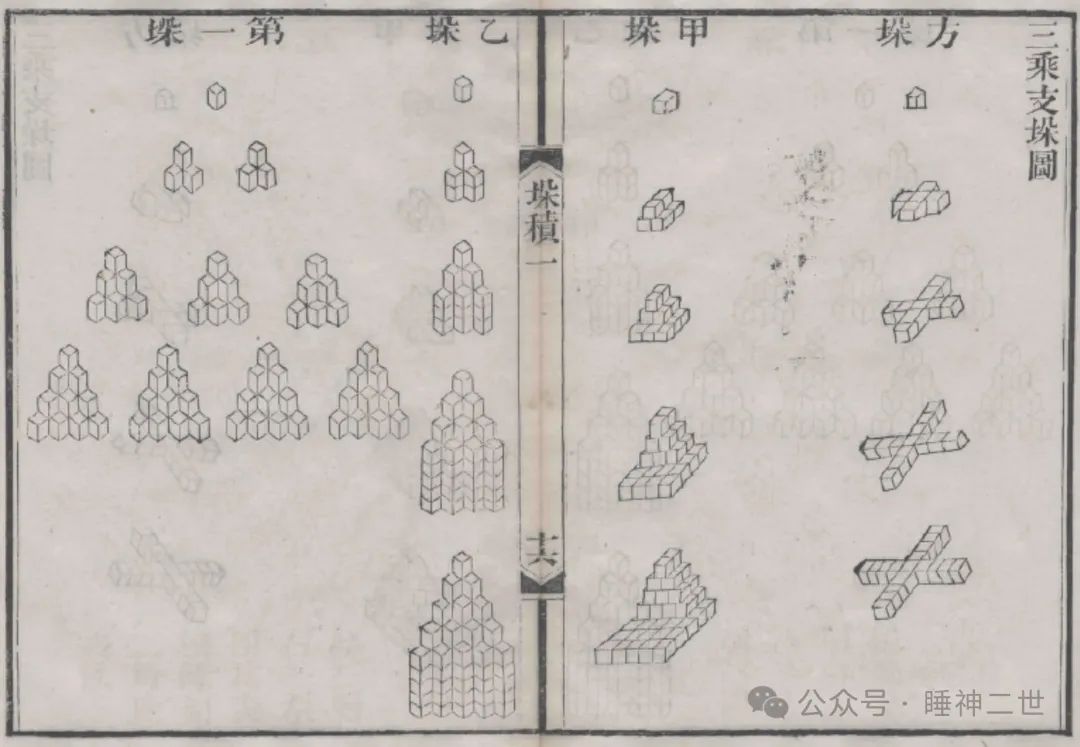
李善兰在《四元解》中使用的方法也有垛积术的思想，一脉贯通。

《方圆阐幽》

《方圆阐幽》是一部篇幅很短的著作，但是却体现了李善兰重要的数学思想。全书包含十个“当知”，构建出他的核心思想“尖锥术”。

第一，当知西人所谓“点”“线”“面”皆不能无体。

第二， 当知体可变为面， 面可变为线……为面便可如纸之薄，为线便可为丝之细，故盈尺之书由叠纸而得，盈丈之绢由积丝而成也。

这里李善兰的阐述与《几何原本》已经截然不同了，他放弃了《几何原本》中最基本的“点者无分，无长短广狭厚薄”、“线有长无广”的定义，把点、线、面都看做某个维度是无穷小的体。

第三， 当知诸乘方有线、面、体循环之理

第四， 当知诸乘方皆可变为面，并皆可变为线

貌似他的思想与《几何原本》是不同的，但是经过我对《几何原本》的学习，我认为李善兰恰恰是深刻理解了徐光启的《几何原本》六卷，才会有这样的数学思想。我在徐光启、利玛窦与《几何原本》（五）中分析过徐版的《几何原本》包含了度与量的关系，研究的是在一定测量精度下的量。而李善兰说“当知诸乘方有线、面、体循环之理”，改变测量精度就可以实现线面体的转换。李善兰把《几何原本》的思想提升到了一个新的高度。

第五， 当知平面尖锥之形

第六， 当知诸乘方皆有尖锥

第七， 当知诸尖锥有积叠之理

这是李善兰独创的尖锥术，而尖锥的构建方法明显来自于《垛积比类》，当n趋近于∞，尖锥就可以用垛积方法来构建和计算。尖锥术可以被看做把测量精度提高到无穷小级别的垛积术。

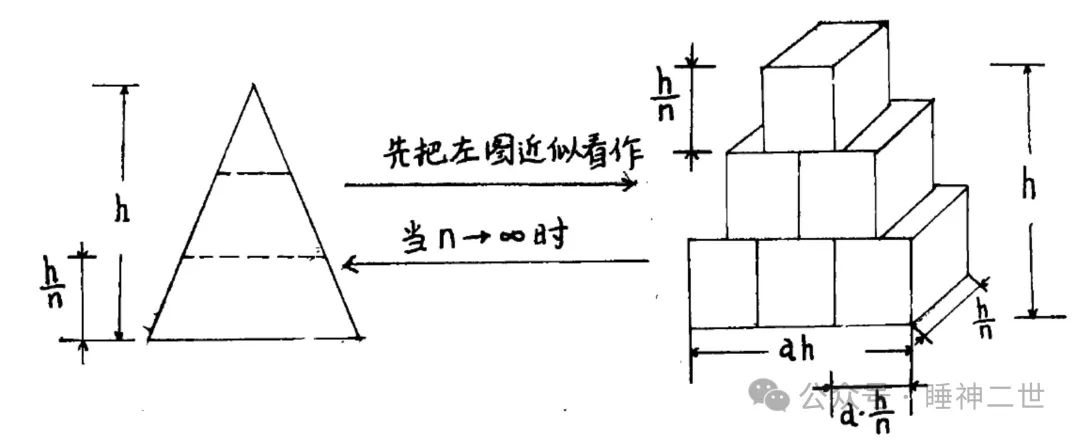
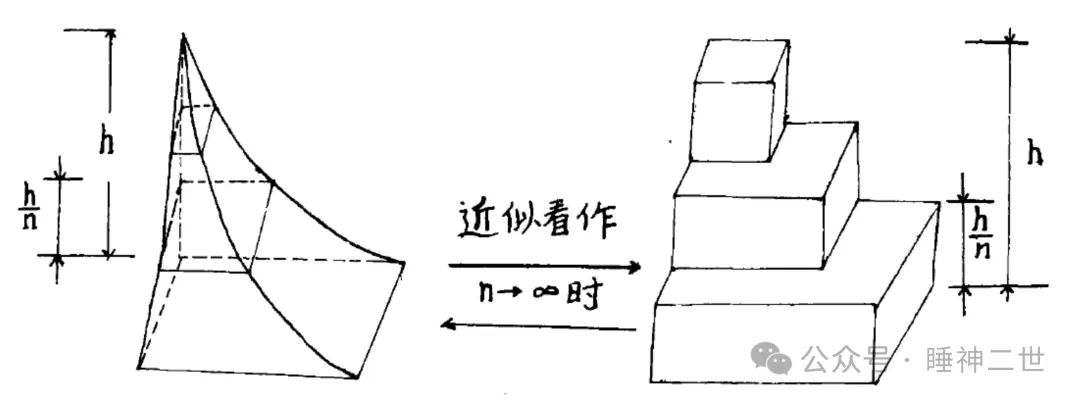
第八， 当知诸尖锥之算法， 以高乘底为实，本乘方数加一为法，除之，得尖锥积

第九， 当知二乘以上尖锥其所叠之面皆可变为线， 面变为线，则诸尖锥皆成平体而曲其边正则曲二边，偏则曲一边，乘益多则曲益甚

第十， 当知诸尖锥即为面，则可并为一尖锥

在平面内诸乘尖锥面皆由底线、高线和尖锥曲线组成一曲边三角形，乘数愈多(即幂次愈高)，尖锥曲线其凹愈甚。这样就建立了尖锥与代数的对应关系，以代数方法描述曲线的几何性质。尖锥术已经具备了解析几何的思想。

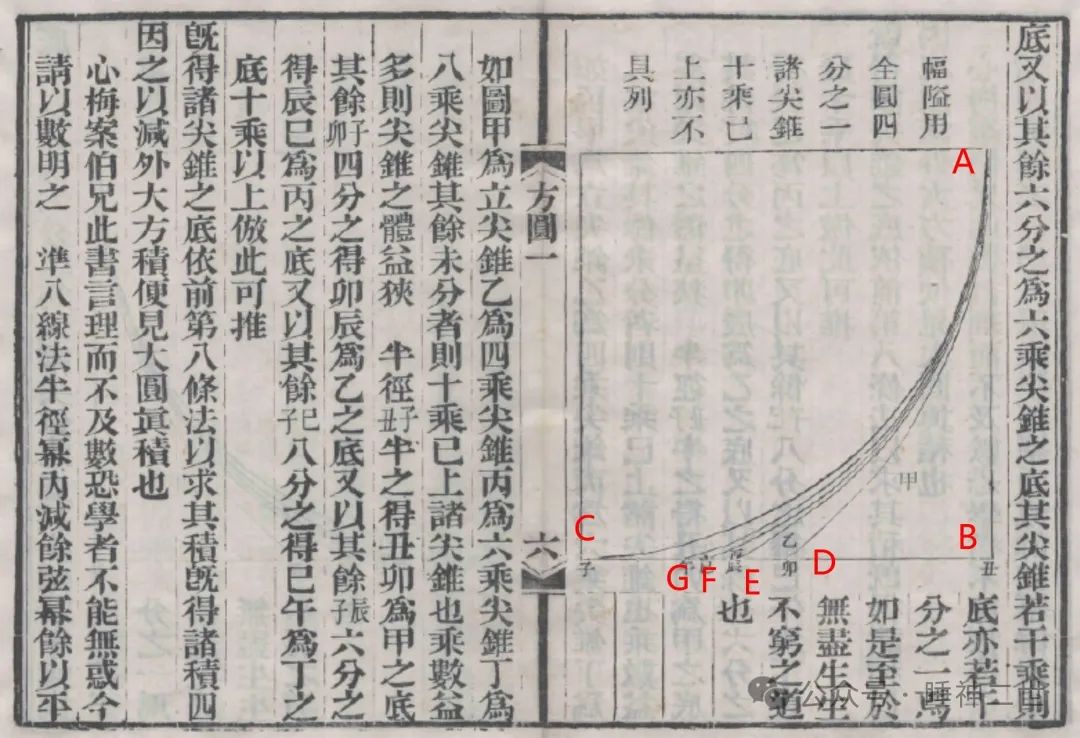
求圆面积是李善兰给出的尖锥术的一个应用示例，欲求圆的面积，只要先求出圆外切正方形与圆之间的尖锥面积，而这个尖锥面积是由一系列小尖锥组合而成，如上图，设边长BC=1，

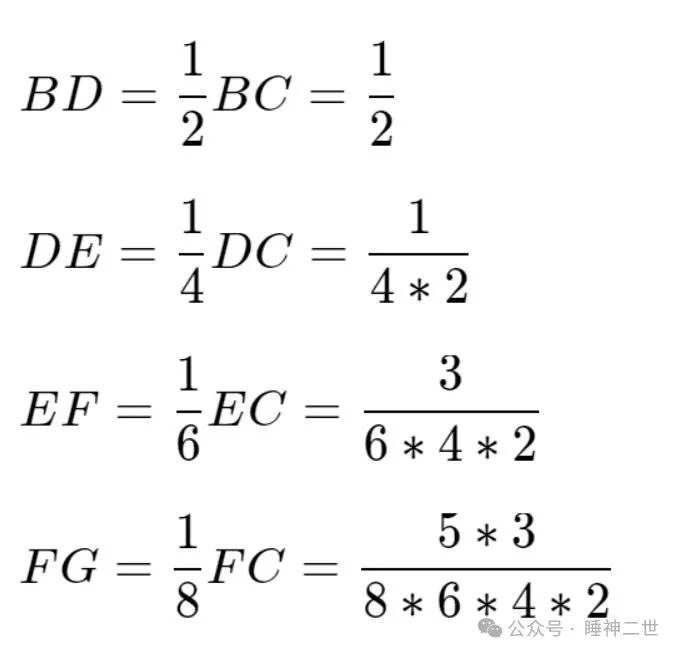
……以此类推，可以得出

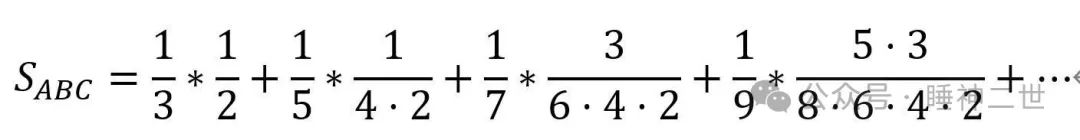
这是一个无穷级数展开式，代入的n数值越大，构建的尖锥数量就越多，结果就越接近真实值。这包涵了微积分的极限概念、无穷小概念、微分思想、积分思想。在嘉兴期间与李善兰交流的数学家们已经具备了这些数学思想，而尖锥术是李善兰独创的方法。

为什么我确定尖锥术可以直接与解析几何相联系？如上图的1/4圆实际已经是一个直角坐标系了，李善兰的求圆面积方法就是用数学方法来实现尖锥无限逼近圆外积。而对于古代学者这个图形的象征性意义更为明显，这是一个天文观测仪器（如下图）。这台仪器的名字叫做“象限仪”，我们学习直角坐标系的四象限，实际这些知识恰恰都来源于古代中国。

《弧矢启秘》

李善兰在《方圆阐幽》中创立了尖锥术，用以求解圆周率，又附带得出了二项平方根的幂级数展开式。在《孤矢启秘》中，又用尖锥术求解三角函数和反三角函数的幂级数展开式。

讨论三角函数的幂级数展开式，必须要回溯一下在中国古代的发展历史。清初数学家梅瑴成，梅文鼎之孙，负责编修《数理精蕴》，在他的著作《赤水遗珍》中提到了三个三角函数的幂级数展开式，梅瑴成称这三个公式来自于法国传教士杜德美，但杜德美并不能解释和证明，被称为“杜氏三术”。

梅瑴成《赤水遗珍》

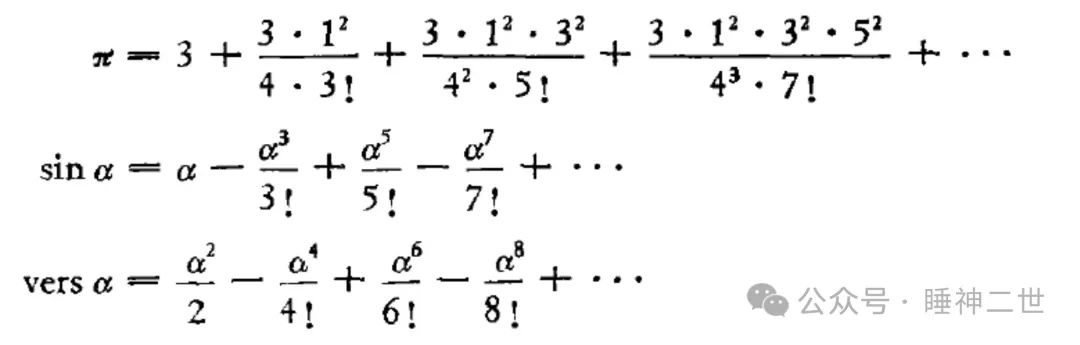
当代的说法是第一个公式“求周径密率捷法”是牛顿于1676 年所创，后二式“求弦矢捷法”是格列哥利(J.Gregory)于1667年所创。

此后数学家明安图创“割圆连比例法”证明了“杜氏三术”(“圆径求周”“弧背求正弦”“弧背求正矢”三式)，并提出了另外六个级数式。明安图得出了正弦、正矢、反正弦、反正矢的幂级数展开式。但是其研究成果却被冠以“杜氏九术”的称呼，明明是中国人的成果也要冠名为西法。

李善兰的好友徐有壬的《测圆密率》中得到了正切函数、反正切函数的幂级数展开式，戴煦在徐有壬的基础上进一步完善了正切函数。徐有壬、戴煦与李善兰都有密切的学术交流。

李善兰《弧矢启秘》用他自创的尖锥术这种解析的方法，配合代数运算，卓有成效地展开了各种三角函数，把自明安图以来对三角函数幂级数展开式的研究大大提高了。伟烈亚力曾说“在题为《弧矢启秘》的论文中,他(李善兰)给出了推演八线互求的新方法，特别是从正割求弧长和从弧长求正割的方法，则是在任何先前本国的工作中尚未给出过的。”也就是说李善兰的成果比徐有壬、戴煦更早，且使用的是独创的方法。

《对数探源》

关于对数的研究，最早要追溯到明末清初，我在《重学》1：清朝科技文化的断崖式衰落 中提到的数学家薛凤祚。《比例对数表》12卷，是中国最早的一部对数专著。此书首次编制了一至二万的常用对数表，并计算到小数第六位。虽然年轻时薛凤祚与传教士有交往，但《比例对数表》是其晚年独立完成的，与传教士无关。

此后梅瑴成在《数理精蕴》中介绍了造常用对数表的三种方法，即“中比例法”、“递次自乘法”和“递次开方法”，并有一至十万的常用对数表，且对数表精确到了小数点后10位。

清末的数学家戴煦对对数有深入研究，著成《对数简法》(1845)，《续对数简法》(1846)，《假数测圆》(1852)，总名《求表捷术》。《畴人传三编》记述了艾约瑟通过李善兰了解到戴煦的《求表捷术》后要登门拜访，被戴煦婉拒，此后艾约瑟把戴的著作引入英国算学工会。这是传教士盗取中国科技成果的又一个实证。

“英吉利人艾约瑟见之(即《求表捷术》)，甚推服,踵门求见，煦引东坡事却焉。艾后转译煦书，入彼国算学公会中，其倾倒如此”——《畴人传三编》

戴煦的《对数简法》中的开方七术，第一术叙述了他的开方法的核心技术内容:

术曰:自一至九为初商根，各自乘以次列之为初商实。以所设方积较初商实，取其稍大于方积者，以其方根为第一数。次以初商实内减方积为减余数。以第一数除之，二除之，为第二数。又以减余数除初商实，所得为每数除法。乃以除法除第二数，一乘之，四除之，为第三数。以除法除第三数，三乘之，六除之，为第四数。以除法除第四数，五乘之，八除之，为第五数。以除法除第五数，七乘之，十除之，为第六数。每数以一、三、五、七、九诸奇数为乘法，以二、四、六、八、十诸偶数为除法，依次递求至应求位数下。第一数恒为正，第二数以下，均为负，并诸负数以减第一正数，得所求

这个方法在今天被称为函数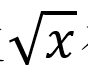在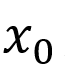点的泰勒级数。此外戴煦还得出了对数换底公式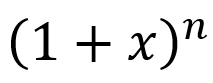，的幂级数展开以及ln（1+x）的麦克劳林级数。

在戴煦《对数简法》完成的同一年（1845年）李善兰完成了《对数探源》。在《对数探源》中，李善兰列出了十个定理来阐述尖锥曲线与对数的代数关系，其使用尖锥术的思想自成体系。而过程的证明仍然是依靠他惯用的垛积术来完成。之后他给出了用无穷级数方法求对数的具体步骤。

以上回顾的著作是李善兰在1845-1846年就已经完成的，其中《对数探源》被收录于钱熙祚的《指海》（1850年），《方圆阐幽》、《弧矢启秘》被收录于钱熙辅的《艺海珠尘》（1851年）。

梳理了李善兰这一时期的著作，我惊奇的发现李善兰对这一时期的所有数学问题都有很深的研究造诣，且他解决问题的思路方法独树一帜自成体系，其学术成果多得惊人，他的著作中以垛积术为基础，以微积分的思想发明了尖锥术。尖锥术已经具备了极限思想、无穷小思想、解析几何思想、微积分思想，并且在研究三角函数、幂函数、对数的无穷级数展开等问题上卓有成效，所欠缺的就是以代数形式来描述它们。

这一时期与李善兰交往密切的数学家如顾观光、徐有壬、戴煦、罗士琳等人也都具备了相当的数学水平，而李善兰是其中最杰出者并取得了非凡的成就。可以清晰地看出李善兰学术思想的形成脉络以及在他以前中国历史上的流传过程，而这恰恰是西方伪史、伪科学家们所不具备的。

这一时期的学术成果为李善兰在墨海书馆所创造的成就奠定了基础。

1852年，李善兰加入了墨海书馆。